Gli assiomi di Euclide
Apparentemente anche lo stesso Euclide non era soddisfatto dalla sua versione dell’assioma delle parallele, perché non vi fece ricorso se non dopo aver dimostrato tutti i teoremi che si potevano provare senza di esso. I postulati di Euclide sono cinque, di cui i primi quattro immediatamente evidenti e praticamente verificabili, sono:
-
Tra due punti qualsiasi è possibile tracciare una e una sola retta;
-
Si può prolungare una retta oltre i due punti indefinitamente;
-
Dato un punto e una lunghezza, è possibile descrivere un cerchio;
-
Tutti gli angoli retti sono uguali.
Il quinto, quello delle parallele, risulta essere non evidente e separato dagli altri quattro:
se una retta taglia altre due rette determinando dallo stesso lato angoli interni la cui somma è minore di quella di due angoli retti, prolungando indefinitamente le due rette, esse si incontreranno dalla parte dove la somma dei due angoli è minore di due angoli retti o come è più comunemente definito secondo l’assioma di Playfair: data una qualsiasi retta r ed un punto P non appartenente ad essa, è possibile tracciare per P una ed una sola retta parallela alla retta r data.
La particolare formulazione dell’assioma da parte di Euclide era un modo per evitare l’affermazione esplicita che esistono coppie di rette infinite perché, se fossero state finite, non avrebbero potuto essere prolungate tanto quanto fosse stato necessario in ogni contesto, considerato che egli dimostrò l’esistenza di rette parallele.
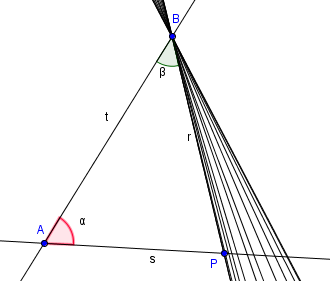
Prendendo in esame questa figura, se si mantengono fisse t ed s e si fa ruotare r in senso antiorario intorno a B, secondo il V postulato r continuerà ad incontrare s finché a+b<180. Possiamo però notare che, al ruotare di r, il punto P si allontana sempre di più da A su s, finendo per uscire dallo schermo e non essere più osservabile. Quindi non è possibile verificare che la retta r non abbia più un punto in comune con s quando a+b=180. Questa proposizione risulta falsa in un universo di dimensioni finite. Immaginiamo infatti che il piano contenente r e P sia limitato alla zona interna ad un cerchio, si vede immediatamente che vi sono molte rette passanti per P che non incontrano r.
 Laboratorio Piano Lauree Scientifiche
Geometrie non Euclidee
Centro Educativo Ignaziano
Palermo
Laboratorio Piano Lauree Scientifiche
Geometrie non Euclidee
Centro Educativo Ignaziano
Palermo
